Solusi Numerik untuk Sistem Persamaan Linear
Contents
Solusi Numerik untuk Sistem Persamaan Linear¶
Suatu sistem persamaan linear (SPL) adalah kumpulan dari sejumlah \(n\) persamaan atau secara matematis dapat ditulis
Di dalam (1), terdapat koefisien \(a_{ij}\), untuk \(i,j = 1,2, \cdots, n\), dan \(b_i\), dan kita perlu untuk mencari unknowns \(x_1, x_2,\cdots, x_n\). SPL (1) juga dapat ditulis dalam bentuk matriks-vektor yaitu
dimana \(A \in \mathbb{R}^{n \times n}\), \(\vec{x} \in \mathbb{R}^n\), dan \(\vec{b} \in \mathbb{R}^n\).
Terdapat dua cara untuk menyelesaikan (1) menggunakan solusi numerik:
Metode Langsung (Naive) (fokus pada analisa error pembulatan)
Metode Iteratif
Selain mencari \(\vec{x}\), permasalahan yang ada di dalam SPL meliputi:
Determinan dari matriks
Invers dari matriks
Tipe-tipe khusus dari matriks:
Matriks Definit Positif
Matriks Tridiagonal
Beberapa metode yang akan dipelajari antara lain:
Eliminasi Gauss
Partial Pivoting
Faktorisasi Matriks
Dekomposisi LU
Matriks Permutasi
Cholesky
Faktorisasi Crout
Sistem Persamaan Linear¶
Kita menggunakan tiga operasi baris untuk menyederhanakan SPL (1):
Persamaan \(E_i\) dapat dikali oleh suatu konstanta \(\lambda\) yang tak nol,yang hasilnya ditempatkan di \(E_i\). Operasi tersebut dinotasikan sebagai \((\lambda E_i) \rightarrow (E_i)\).
Persamaan \(E_j\) dapat dikali oleh suatu konstanta \(\lambda\) dan ditambahkan ke persamaan \(E_i\), yang hasilnya ditempatkan di \(E_i\). Operasi ini dapat dinotasikan sebagai \((E_i + \lambda E_j) \rightarrow (E_i)\).
Persamaan \(E_i\) dan \(E_j\) dapat ditukar urutannya atau dapat ditulis \((E_i) \leftrightarrow (E_j)\).
Contoh 1:¶
Diberikan SPL
Tujuannya adalah mencari nilai dari \(x_1, x_2, x_3\), dan \(x_4\).
Pertama, kita eliminasi \(x_1\) dari persamaan \(E_2, E_3\), dan \(E_4\) dengan cara:
\((E_2-2E_1)\rightarrow(E_2)\)
\((E_3-3E_1)\rightarrow(E_3)\)
\((E_4+E_1)\rightarrow(E_4)\)
akan menghasilkan sistem persamaan baru
Di dalam sistem persamaan baru ini, kemudian, kita eliminasi \(x_2\) dari \(E_3\) dan \(E_4\) dengan cara:
\((E_3-4E_2)\rightarrow(E_3)\)
\((E_4+3E_2)\rightarrow(E_4)\),
sehingga menghasilkan
SPL (2) sudah menjadi bentuk tereduksi dan untuk mencari nilai unknowns tersebut digunakan proses subtitusi mundur. Karena \(E_4\) bernilai \(x_4 = 1\), kita selesaikan \(E_3\) untuk mencari \(x_3\)
Dilanjutkan untuk \(E_2\)
dan \(E_1\)
Jadi solusinya adalah \(x_1 = -1, x_2 = 2, x_3 = 0\), dan \(x_4 = 1\).
Desain Algoritma untuk Eliminasi Gauss¶
Agar dapat mempermudah pengimplementasiannya ke dalam bahasa pemrograman, SPL(1) diubah ke dalam bentuk augmented,
atau dapat ditulis dalam bentuk augmented matrix \(C\)
Untuk menyelesaikan SPL tersebut, kita gunakan Eliminasi Gauss yang desain algoritmanya adalah sebagai berikut:
Buat sistem segitiga atas menggunakan eliminasi maju.
Kita lakukan eliminasi \(x_1\) dari persamaan \(E_2\), \(E_3\), \(E_4, ..., E_n\) menghasilkan SPL baru, lakukan eliminasi \(x_2\) dari persamaan \(E_3, E_4, ..., E_n\), dst. sampai \(x_{n-1}\) dari persamaan \(E_n\) atau dapat ditulis dalam bentuk algoritma
for i=1 to n for j=i+1 to n (E_j) <- (E_j) - (a_{ji}/a_{ii})*(E_i)
Maka algoritma ini akan menghasilkan sistem segitiga atas
Catatan bahwa nilai dari koefisien \(a_{i,j+1}\) di (4) berbeda dari (3).
Subtitusi mundur
Lakukan subtitusi mundur untuk mendapatkan solusinya.
x_n = a_{n, n+1} / a_{nn}
for i = n-1 to 1
x_i = 1/a_{ii} (a_{i, n+1} - sum(a_{ij}*x_j))
Implementasi di Python¶
SPL biasanya diubah ke dalam bentuk augmented matrix, agar lebih mudah untuk mengimplementasikannya.
import numpy as np
import matplotlib.pyplot as plt
def eliminasi_gauss(A, b):
# Gabung matriks A dan b sehingga membentuk augmented matrix A_c
A_c = np.c_[A,b]
# Jumlah baris dari A
n = A.shape[0]
# Lakukan eliminasi maju
for i in range(n):
faktor = A_c[i+1:, i]/A_c[i,i]
A_c[i+1:] -= faktor[:, np.newaxis] * A_c[i]
x = np.zeros_like(b, dtype=np.float64)
# Lakukan subtitutsi mundur
x[-1] = A_c[-1,-1]/A_c[-1,-2]
for i in range(n-2, -1, -1):
x[i] = 1/A_c[i,i] * (A_c[i,-1] - np.dot(A_c[i,i:-1], x[i:]))
return x
A = np.array([[1, 1, 0, 3],
[2, 1, -1, 1],
[3, -1, -1, 2],
[-1, 2, 3, -1]], dtype=np.float64)
b = np.array([4, 1, -3, 4], dtype=np.float64)
sol = eliminasi_gauss(A,b)
sol
array([-1., 2., 0., 1.])
Contoh 2¶
A = np.array([[1e-17, -1],
[1,2]], dtype=np.float64)
b = np.array([-1, 3], dtype=np.float64)
sol = eliminasi_gauss(A,b)
sol
array([0., 1.])
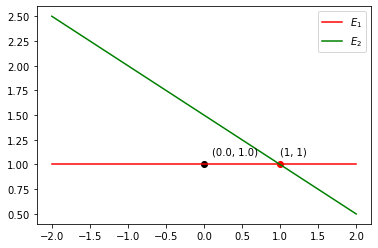
# plot SPL
x = np.linspace(-2, 2)
f1 = 1 + 1e-17*x
f2 = (3 - x)/2
plt.plot(x, f1, color='red', label='$E_1$')
plt.plot(x, f2, color='green', label='$E_2$')
# solusi eliminasi
plt.scatter(sol[0], sol[1], marker='o', color='black')
plt.annotate('({}, {})'.format(sol[0], sol[1]), sol+0.1)
# solusi eksak
plt.scatter(1, 1, marker='o', color='red')
plt.annotate('(1, 1)', (1,1+0.1))
plt.legend();
detA = np.linalg.det(A) # Determinan A
detA
1.0
condition_number = np.linalg.cond(A) # Condition Number A
condition_number
5.828427124746189
Dari Contoh 2 terlihat bahwa condition number dari A adalah 5.8284 mengindikasikan bahwa matriks tersebut ill-condition atau hampir singular. Matriks yang ill-condition dapat terjadi karena error pembulatan, sehingga solusi numerik yang dihasilkan salah. Walaupun kita tahu bahwa determinan dari A tak nol artinya SPL pada Contoh 2 memiliki solusi tunggal.
If the condition number is not too much larger than one, the matrix is well-conditioned, which means that its inverse can be computed with good accuracy. If the condition number is very large, then the matrix is said to be ill-conditioned. Practically, such a matrix is almost singular, and the computation of its inverse, or solution of a linear system of equations is prone to large numerical errors. A matrix that is not invertible has condition number equal to infinity. (https://en.wikipedia.org/wiki/Condition_number)
Eliminasi Gauss dengan Scaled Partial Pivoting¶
Untuk menghindari hal tersebut, kita memerlukan penukaran baris di A.
A[[0,1],:] = A[[1,0],:]
b[[0,1]] = b[[1,0]]
print("A = ", A)
print("b = ", b)
A = [[ 1.e+00 2.e+00]
[ 1.e-17 -1.e+00]]
b = [ 3. -1.]
sol = eliminasi_gauss(A, b)
sol
array([1., 1.])
📌 Jadi, kapan kita perlu menukar baris?
Mari kita lihat SPL berikut
Asumsikan bahwa kita telah mendapatkan nilai dari \(x_2\) dan mengandung error pembulatan (round-off error), \(\hat{x}_2 = x_2 + \varepsilon_2\). Kemudian kita hitung \(x_1\) dengan \(\hat{x}_2\):
dengan demikian kita dapatkan \(\varepsilon_1 = \frac{a_{12}}{a_{11}} \varepsilon_2\). Error di \(x_2\) terpropagasi dengan suatu faktor \(\frac{a_{12}}{a_{11}}\). Kasus ini disebut juga dengan error terpropagasi (propagated error). Untuk menghasilkan hasil yang terbaik, kita menginginkan nilai dari \(|a_{11}|\) sebesar mungkin.
Algoritma Eliminasi Gauss dengan Scaled Partial Pivoting¶
Dari kasus tersebut, kita memerlukan teknik scaled partial pivoting. Idenya adalah mencari skala terbesar dari masing-masing koefisien di setiap persamaan, \(max_{k \leq i \leq n} |a_{ik}|\) untuk \(a_{ii}\), kemudian cari mana baris yang memiliki skala terbesar dan lakukan penukaran baris. Untuk lebih jelasnya, kita lihat algoritma berikut:
Algoritma: Eliminasi_Gauss_Scaled_Pivoting(A, b)
INPUT: A` adalah matriks augmented [A,b], n adalah ukuran dari A.
OUTPUT: variabel x
1. Mencari skala terbesar dari setiap baris
for i=1 to n
s[i] = max(|a[i,j]|), j = 1,2,..,n
if s[i] == 0
print('tidak ada solusi tunggal')
for i=1 to n
2. Mencari indeks dari baris yang memiliki skala terbesar dan lakukan penukaran baris:
for i=1 to n-1
p = argmax(|a[k, i]|/s[i]), k = 1,2,...,n (mencari indeks)
if p ~= i
A`[[i,p]] <=> A`[[p,i]] (lakukan penukaran baris)
s[i] <=> s[p] (lakukan penukaran nilai skala)
3. Selanjutnya, lakukan eliminasi maju seperti pada algoritma sebelumnya.
endfor
4. Lakukan subtitusi mundur.
Contoh 3¶
Diberikan SPL
Dari SPL tersebut, pertama kita cari skala terbesar di setiap baris/persamaan. Untuk baris pertama \(E_1\):
baris kedua \(E_2\):
dan, baris ketiga \(E_3\):
Kemudian kita cari baris yang akan ditukar:
dari sini kita dapatkan bahwa baris kedua \(E_2\) yang memiliki nilai terbesar. Dengan demikian, lakukan penukaran \(E_1 \leftrightarrow E_2\). Sehingga SPLnya menjadi
Kemudian kita lakukan eliminasi maju untuk mengeliminasi \(x_1\) dari \(E_2\) dan \(E_3\)
\((E_2 - \frac{1}{3} E_1) \rightarrow (E_2)\)
\((E_3 - \frac{2}{3} E_1) \rightarrow (E_3)\).
Sehingga didapat SPL baru, yaitu
dan kita cari lagi baris yang akan ditukar dari SPL baru tersebut:
sehingga kita tukar \(E_1 \leftrightarrow E_3\), maka didapat SPL baru selanjutnya
dan lakukan eliminasi maju untuk mengeliminasi \(x_2\) dari \(E_1\):
\((E_1 - \frac{1}{11} E_3) \rightarrow (E_1)\)
sehingga didapatkan SPL:
Kemudian lakukan subtitusi mundur, sehingga didapatkan \(x_1 = 1, x_2 = 0, x_3 = 2\).
def eliminasi_gauss_pivoting(A,b):
A_c = np.c_[A,b]
n = len(A)
s = np.zeros(n)
# Mencari skala terbesar
for i in range(n):
s[i] = max(np.abs(A_c[i,:n]))
for i in range(n):
# Lakukan penukaran baris
for k in range(n-1):
p = np.argmax(np.abs(A_c[k:n, k])/s[k:n]) + k
if p != k:
A_c[[k,p],:] = A_c[[p,k],:]
s[k], s[p] = s[p], s[k]
# Lakukan eliminasi maju
faktor = A_c[i+1:, i]/A_c[i,i]
A_c[i+1:] -= faktor[:, np.newaxis] * A_c[i]
x = np.zeros_like(b, dtype=np.float64)
# Lakukan subtitutsi mundur
x[-1] = A_c[-1,-1]/A_c[-1,-2]
for i in range(n-2, -1, -1):
x[i] = 1/A_c[i,i] * (A_c[i,-1] - np.dot(A_c[i,i:-1], x[i:]))
return x
A = np.array([[1,2,1],
[3,4,0],
[2,10,4]], dtype=np.double)
b = np.array([3,3,10], dtype=np.double)
eliminasi_gauss_pivoting(A,b)
array([1., 0., 2.])
Contoh 4¶
Dari Contoh 2, kita gunakan scaled partial pivoting
A = np.array([[1e-17, -1],
[1,2]], dtype=np.float64)
b = np.array([-1, 3], dtype=np.float64)
x_pivoting = eliminasi_gauss_pivoting(A,b)
x_pivoting
array([1., 1.])
Contoh 5¶
A = np.array([[1, 1e17],
[1, 1e-17]], dtype=np.double)
b = np.array([1e17, 1], dtype=np.double)
np.linalg.cond(A)
9.999999999999997e+16
np.linalg.det(A)
-1.000000000000001e+17
x = eliminasi_gauss(A,b)
x
array([0., 1.])
x_pivoting = eliminasi_gauss_pivoting(A, b)
x_pivoting
array([1., 1.])
rankA = np.linalg.matrix_rank(A, tol=1e-17)
rankA
2
