Contents

Solusi Numerik Persamaan Differensial Biasa

Solusi Numerik Persamaan Differensial Biasa

Pendahuluan

Persamaan Differensial (PD) dapat didefinisikan sebagai suatu persamaan yang berisi satu atau lebih turunan. Kondisi awal (initial condition) adalah nilai dari variabel terikatnya ketika variabel bebasnya bernilai nol. Solusi dari PD adalah suatu fungsi yang mememuhi persamaannya dan kondisinya.

Misalkan perubahan populasi penduduk dari waktu ke waktu di kota Jakarta digambarkan oleh persamaan

\[ \frac{dP}{dt} = rP \]

dimana \(r\) adalah tingkat pertumbuhan populasi penduduknya dan \(P\) adalah jumlah populasi penduduknya pada waktu ke \(t\). Kemudian diketahui pertumbuhan populasi per tahunnya adalah 10% dan penduduk di kota Jakarta berjumlah 10 juta jiwa pada saat ini. Maka perubahan populasi penduduk dari waktu ke waktu dapat digambarkan dengan persamaan

\[ \frac{dP}{dt} = 0.10P. \]

Dengan demikian, solusi dari PD tersebut adalah suatu fungsi, \(P(t)\) yang memiliki turunan \(0.10P(t)\) dengan \(P(0) = 10^{6}\). Untuk mencari solusi analitiknya, pertama

\[\begin{split} \begin{array}{ll} \frac{1}{P} dP &=& 0.10 dt \\ \int \frac{1}{P} dP &=& \int 0.10 dt\\ \ln{P} &=& 0.10t + C \end{array} \end{split}\]

sehingga

\[ P(t) = e^{0.10t} e^C. \]

atau

\[ P(t) = ke^{0.10t} \]

dimana \(k = e^C\).

Jika diketahui \(P(0)=10^{6}\), maka

\[ 10^{6} = ke^{0.10*0} = k * 1 = k. \]

Sehingga solusinya adalah

\[ P(t) = 10^{6}e^{0.10t} \]

atau secara umum dapat ditulis

\[ P(t) = P_0 e^{0.10t} \]

untuk suatu nilai kondisi awal \(P_0\).

Contoh 1.

Misalkan \(y = y(t)\) merupakan suatu fungsi dari \(t\), contoh PDB dari fungsi tersebut diantaranya \(y' = y^2\), \(y'' + y.y' + 4 = 0\), dan lainnya.

Masalah dalam PDB dibagi menjadi dua yaitu Masalah Nilai Awal (MNA) dan Masalah Syarat Batas (MSB). MNA untuk orde pertama PDB didefinisikan:

\[ \begin{matrix} y' = f(t,y), & y(t_0)=y_0 \end{matrix} \]

Sebagai contoh:

\[\begin{split} \begin{matrix} y' = y+1, & y(t_0) = 0. & \text{Solusi:} & y(t) = e^t - 1, \\ y' = 2, & y(t_0) = 0. & \text{Solusi:} & y(t) = 2t. \end{matrix} \end{split}\]

Dalam banyak masalah, solusi eksak sangat sulit untuk didapatkan.

Solusi Numerik: Diberikan

\[ \begin{matrix} y' = f(t,y), & y(t_0)=y_0. \end{matrix} \]

Cari \(y_n = y(t_n)\) untuk \(n = 1,2,\dots ,N\) dan \(t_0 < t_1 < \dots <t_N\). Disini \(t_N\) menyatakan waktu akhir komputasi. Ambil step waktu yang seragam: Misalkan \(h\) adalah panjang step waktu

\[ \begin{matrix} t_{n+1} - t_{n} = h, & t_k = t_0 + kh, & k=1,2,\dots,N \end{matrix} \]

Metode Deret Taylor (MDT)

Diberikan

\[ \begin{matrix} y'=f(t,y(t)), & y(t_0)=y_0 \end{matrix}. \]

Misalkan kita ingin mencari \(y_1 = y(t_1) = y(t_0+h)\). Ekspansi Taylornya adalah

\[ y(t_0 + h) = y(t_0) + hy'(t_0) + \frac{1}{2}h^2y''(t_0) + \dots = \sum_{m=0}^{\infty} \frac{1}{m!} h^m y^{(m)} (t_0). \]

MDT untuk order \(m\): Ambil suku ke \((m+1)\) pertama dari Ekspansi Taylor

\[ y(t_0 + h) = y(t_0) + hy'(t_0) + \frac{1}{2}h^2y''(t_0) + \dots + \frac{1}{m!} h^m y^{(m)} (t_0). \]

Error di masing-masing step:

\[ y(t_0 + h) - y_1 = \sum_{k=m+1}^{\infty} \frac{1}{k!} h^k y^{(k)} (t_0) = \frac{1}{(m+1)!} h^{m+1} y^{(m+1)} (\xi) \]

untuk suatu \(\xi \in (t_0, t_1).\)

Untuk \(m=1\), kita dapatkan Metode Euler:

\[ y_1 = y_0 + hy'(t_0) = y_0 + hf(t_0,x_0). \]

Bentuk umum untuk \(k\) step:

\[ \begin{matrix} y_{k+1} = y_k + hf(t_k,x_k), & k = 1,2,\dots \end{matrix} \]

Untuk \(m=2\), kita dapatkan

\[ y_1 = y_0 + hy'(t_0) + \frac{1}{2} h^2 y''(t_0) \]

Bentuk \(y''(t_0)\) dapat dicari menggunakan

\[\begin{split} \begin{matrix} y''(t_0) & = \frac{d}{dt} f(t_0, y(t_0)) \\ & = f_t(t_0,y_0) + f_y(t_0,y_0) y'(t_0) \\ & = f_t(t_0,y_0) + f_y(t_0,y_0)f(t_0,y_0) \end{matrix} \end{split}\]

sehingga kita dapatkan

\[ y_1 = y_0 + hy'(t_0) + \frac{1}{2} h^2 \left[f_t(t_0,y_0) + f_y(t_0,y_0)f(t_0,y_0)\right] \]

Bentuk umum untuk \(k\) step:

\[ \begin{matrix} y_{k+1} = y_k + hy'(t_k) + \frac{1}{2} h^2 \left[f_t(t_k,y_k) + f_y(t_k,y_k)f(t_k,y_k)\right], & k=1,2,\dots \end{matrix} \]

Contoh 2. Terapkan MDT dengan \(m=1,2,3\) untuk

\[ \begin{matrix} y' = -y + e^{-t}, & y(0)=0. \end{matrix} \]

(Solusi eksaknya adalah \(y(t)=te^{-t}\).)

Jawaban. Diberikan inisial data \(y_0 = 0\). Untuk \(m=1\), kita dapatkan

\[ \begin{matrix} y_{k+1} = y_k + h \left( -y_k + e^{-t_k} \right), & k=1,2,\dots \end{matrix} \]

Untuk \(m=2\) dan \(m=3\), kita cari terlebih dahulu \(y''\) dan \(y'''\) dengan cara

\[ y''= \left( -y + e^{-t} \right)^{'} = -y' - e^{-t} = y - e^{-t} - e^{-t} = y - 2e^{-t}. \]
\[ y''' = \left( y - 2e^{-t} \right)^{'} = -y' + 2e^{-t} = y - e^{-t} + 2e^{-t} = y + e^{-t}. \]

Sehingga bentuk iteratif untuk \(m=2\) menjadi

\[\begin{split} \begin{matrix} y_{k+1} & = & y_k + hy'_k + \frac{1}{2} h^2 y''_k & \\ & = & y_k + h(-y_k + e^{-t_k}) + \frac{1}{2} h^2 (y_k - 2e^{-t_k}) & k = 1,2,\dots. \\ \end{matrix} \end{split}\]

dan untuk \(m=3\) adalah

\[\begin{split} \begin{matrix} y_{k+1} & = & y_k + hy'_k + \frac{1}{2} h^2 y''_k & \\ & = & y_k + h(-y_k + e^{-t_k}) + \frac{1}{2} h^2 (y_k - 2e^{-t_k}) + \frac{1}{6} h^3 (y_k + e^{-t_k}) & k = 1,2,\dots. \\ \end{matrix} \end{split}\]

Penerapan. Kita terapkan bentuk iteratif MDT untuk \(m=1\) dan \(m=2\) pada Contoh 2 menggunakan Python 3. Langkah pertama kita definisikan library yang kita pakai,

import numpy as np
import math
import matplotlib.pyplot as plt

h = 0.1
T = 2

N = int(T/h)
t = np.zeros(N+1)
y_m1 = np.zeros(N+1)
y_m2 = np.zeros(N+1)
y_m3 = np.zeros(N+1)
y_a = np.zeros(N+1)

for k in range(N):
    t[k+1] = t[0] + (k+1)*h
    y_a[k+1] = t[k+1]*math.exp(-t[k+1])
    y_m1[k+1] = y_m1[k] + h*(-y_m1[k] + math.exp(-t[k]))
    y_m2[k+1] = y_m2[k] + h*(-y_m2[k] + math.exp(-t[k])) + 0.5*(h**2)*(y_m2[k] - 2*math.exp(-t[k]))

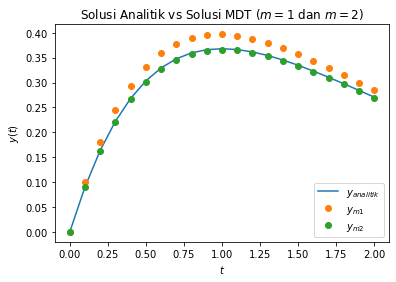
plt.title('Solusi Analitik vs Solusi MDT ($m=1$ dan $m=2$)')
plt.xlabel('$t$')
plt.ylabel('$y(t)$')

plt.plot(t,y_a, label="$y_{analitik}$")
plt.plot(t,y_m1, 'o', label="$y_{m1}$")
plt.plot(t,y_m2, 'o', label="$y_{m2}$")

plt.legend(loc=4);
../_images/Metode_Deret_Taylor_17_0.png 
error_m1 = abs(y_a-y_m1)
error_m2 = abs(y_a-y_m2)

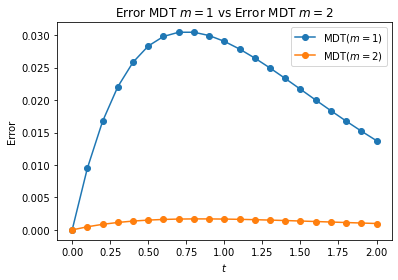
plt.title('Error MDT $m=1$ vs Error MDT $m=2$')
plt.xlabel('$t$')
plt.ylabel('Error')

plt.plot(t,error_m1, '-o', label="MDT($m=1$)")
plt.plot(t,error_m2, '-o', label="MDT($m=2$)")

plt.legend();
../_images/Metode_Deret_Taylor_18_0.png

Contoh 3. Terapkan MDT dengan \(m=1,2,3,4\) untuk

\[ \begin{matrix} y'=y, & y(0)=1 \end{matrix} \]

(Solusi eksaknya adalah \(y(t)=e^t\).)

Jawaban. Perhatikan bahwa

\[ \begin{matrix} y''=y'=y, & y'''=y''=y, & \dots, & y^{(m)} = y. \end{matrix} \]

Diberikan inisial \(y_0=1\), maka kita dapatkan

\[\begin{split} \begin{matrix} m=1: & y_{k+1} = y_k + hy_k = (1+h)y_k \\ m=2: & y_{k+1} = y_k + hy_k + \frac{1}{2} h^2 y_k = (1+h+\frac{1}{2} h^2)y_k \\ m=3: & y_{k+1} = y_k + hy_k + \frac{1}{2} h^2 y_k + \frac{1}{6} h^3 y_k = (1+h+\frac{1}{2}h^2+\frac{1}{6} h^3)y_k \\ m=4: & y_{k+1} = y_k + hy_k + \frac{1}{2} h^2 y_k + \frac{1}{6} h^3 y_k + \frac{1}{24} h^4 y_k = (1+h+\frac{1}{2}h^2+\frac{1}{6} h^3 + \frac{1}{24} h^4)y_k \end{matrix} \end{split}\]

Penerapan.

h = 0.1
T = 2

N = int(T/h)
t = np.zeros(N+1)
y_m1 = np.zeros(N+1)
y_m2 = np.zeros(N+1)
y_m3 = np.zeros(N+1)
y_m4 = np.zeros(N+1)
y_a = np.zeros(N+1)

y_a[0] = 1
y_m1[0] = 1
y_m2[0] = 1
y_m3[0] = 1
y_m4[0] = 1


for k in range(N):
    t[k+1] = t[0] + (k+1)*h
    y_a[k+1] = math.exp(t[k+1])
    y_m1[k+1] = (1+h)*y_m1[k]
    y_m2[k+1] = (1 + h + (1/2) * (h**2)) * y_m2[k]
    y_m3[k+1] = (1 + h + (1/2) * (h**2) + (1/6) * (h**3)) * y_m3[k]
    y_m4[k+1] = (1 + h + (1/2) * (h**2) + (1/6) * (h**3) + (1/24) * (h**4)) * y_m4[k] 

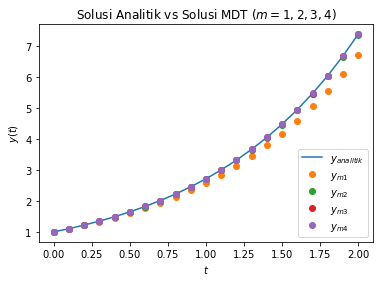
plt.title('Solusi Analitik vs Solusi MDT ($m=1,2,3,4$)')
plt.xlabel('$t$')
plt.ylabel('$y(t)$')

plt.plot(t,y_a, label="$y_{analitik}$")
plt.plot(t,y_m1, 'o', label="$y_{m1}$")
plt.plot(t,y_m2, 'o', label="$y_{m2}$")
plt.plot(t,y_m3, 'o', label="$y_{m3}$")
plt.plot(t,y_m4, 'o', label="$y_{m4}$")

plt.legend(loc=4);
../_images/Metode_Deret_Taylor_24_0.png 
error_m1 = abs(y_a-y_m1)
error_m2 = abs(y_a-y_m2)
error_m3 = abs(y_a-y_m3)
error_m4 = abs(y_a-y_m4)

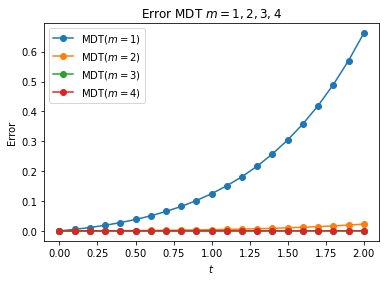
plt.title('Error MDT $m=1,2,3,4$')
plt.xlabel('$t$')
plt.ylabel('Error')

plt.plot(t,error_m1, '-o', label="MDT($m=1$)")
plt.plot(t,error_m2, '-o', label="MDT($m=2$)")
plt.plot(t,error_m3, '-o', label="MDT($m=3$)")
plt.plot(t,error_m4, '-o', label="MDT($m=4$)")

plt.legend();
../_images/Metode_Deret_Taylor_25_0.png

Contoh 3. Terapkan MDT dengan \(m=1,2,3,4\) untuk

\[ \begin{matrix} y'=\sin(t)+e^{-t}, & y(0)=0 \end{matrix} \]

(Solusi eksaknya adalah \(y(t) = -e^{-t} -\cos(t) + 2.)\)

Jawaban. Perhatikan bahwa

\[\begin{split} \begin{matrix} y''=\cos{t}-e^{-t},\\ y'''=-\sin{t}+e^{-t}, \text{dan}\\ y^{(iv)} = -\cos{t}-e^{-t}. \end{matrix} \end{split}\]

Bentuk iteratif untuk \(m=1\) adalah

\[ y_{k+1} = y_k + h \left[ \sin(t_k) + e^{-t_k} \right], \]

untuk \(m=2\)

\[ y_{k+1} = y_k + h \left[ \sin(t_k) + e^{-t_k} \right] + \frac{h^2}{2} \left[ \cos(t_k)-e^{-t_k} \right], \]

untuk \(m=3\)

\[ y_{k+1} = y_k + h \left[ \sin(t_k) + e^{-t_k} \right] + \frac{h^2}{2} \left[ \cos(t_k)-e^{-t_k} \right] - \frac{h^3}{6} \left[ \sin(t_k) - e^{-t_k} \right], \text{dan} \]

untuk \(m=4\)

\[ y_{k+1} = y_k + h \left[ \sin(t_k) + e^{-t_k} \right] + \frac{h^2}{2} \left[ \cos(t_k)-e^{-t_k} \right] - \frac{h^3}{6} \left[ \sin(t_k) - e^{-t_k} \right] - \frac{h^4}{24} \left[ \cos(t_k) + e^{-t_k} \right] \]
h = 0.2*math.pi
T = 5*math.pi

N = int(T/h)
t = np.zeros(N+1)
y_m1 = np.zeros(N+1)
y_m2 = np.zeros(N+1)
y_m3 = np.zeros(N+1)
y_m4 = np.zeros(N+1)
y_a = np.zeros(N+1)

y_a[0] = 0
y_m1[0] = 0
y_m2[0] = 0
y_m3[0] = 0
y_m4[0] = 0


for k in range(N):
    t[k+1] = t[0] + (k+1)*h
    y_a[k+1] = - math.exp(-t[k+1]) - math.cos(t[k+1]) + 2
    y_m1[k+1] = y_m1[k] + h*(math.sin(t[k]) + math.exp(-t[k]))
    y_m2[k+1] = y_m2[k] + h*(math.sin(t[k]) + math.exp(-t[k])) + (1/2) * (h**2) * (math.cos(t[k]) - math.exp(-t[k])) 
    y_m3[k+1] = y_m3[k] + h*(math.sin(t[k]) + math.exp(-t[k])) + (1/2) * (h**2) * (math.cos(t[k]) - math.exp(-t[k])) - (1/6) * (h**3) * (math.sin(t[k]) - math.exp(-t[k]))
    y_m4[k+1] = y_m4[k] + h*(math.sin(t[k]) + math.exp(-t[k])) + (1/2) * (h**2) * (math.cos(t[k]) - math.exp(-t[k])) - (1/6) * (h**3) * (math.sin(t[k]) - math.exp(-t[k])) - (1/24) * (h**4) * (math.cos(t[k]) + math.exp(-t[k]))  

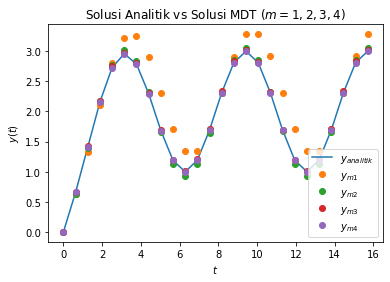
plt.title('Solusi Analitik vs Solusi MDT ($m=1,2,3,4$)')
plt.xlabel('$t$')
plt.ylabel('$y(t)$')

plt.plot(t,y_a, label="$y_{analitik}$")
plt.plot(t,y_m1, 'o', label="$y_{m1}$")
plt.plot(t,y_m2, 'o', label="$y_{m2}$")
plt.plot(t,y_m3, 'o', label="$y_{m3}$")
plt.plot(t,y_m4, 'o', label="$y_{m4}$")

plt.legend(loc=4);
../_images/Metode_Deret_Taylor_30_0.png 
error_m1 = abs(y_a-y_m1)
error_m2 = abs(y_a-y_m2)
error_m3 = abs(y_a-y_m3)
error_m4 = abs(y_a-y_m4)

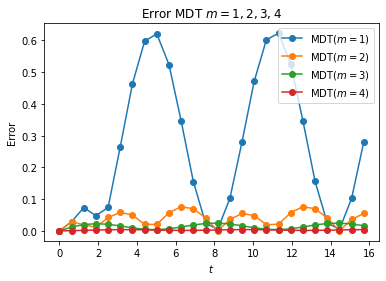
plt.title('Error MDT $m=1,2,3,4$')
plt.xlabel('$t$')
plt.ylabel('Error')

plt.plot(t,error_m1, '-o', label="MDT($m=1$)")
plt.plot(t,error_m2, '-o', label="MDT($m=2$)")
plt.plot(t,error_m3, '-o', label="MDT($m=3$)")
plt.plot(t,error_m4, '-o', label="MDT($m=4$)")

plt.legend(loc=1);
../_images/Metode_Deret_Taylor_31_0.png

Analisis Error. Diberikan PDB

\[ \begin{matrix} y'=f(t,y), & y(t_0)=y_0 \end{matrix} \]

Error pemotongan lokal (error di tiap step waktu) untuk MDT untuk order ke \(m\) adalah

\[ \begin{matrix} e_L^{(k)} = \left| x_{k+1} - x(t_k+h) \right| = \left| \frac{h^{m+1}}{(m+1)!} x^{(m+1)} (\xi) \right|, \end{matrix} \]

untuk \(\xi \in \left( t_k, t_{k+1} \right)\). Kita tahu bahwa

\[ x^{(m+1)} = \frac{d^mf}{dt^m}. \]

Sekarang asumsikan bahwa

\[ \left| \frac{d^mf}{dt^m} \leq M \right|. \]

Dengan demikian kita dapatkan

\[ e_L^{(k)} \leq \frac{M}{(m+1)!} h^{m+1} = O(h^{m+1}). \]

previous

Masalah di Interpolasi Polinomial

next

Metode Runge-Kutta