Sistem Persamaan Differensial
Contents
Sistem Persamaan Differensial¶
Contoh 1: Hukum Kirchhoff¶
Hukum Kirchhoff menyatakan jumlah setiap perubahan tegangan sesaat di sekitar rangkaian tertutup adalah nol. Hukum ini mengimplikasikan bahwa arus \(I(t)\) dalam rangkaian tertutup yang mengandung resistor \(R\) ohm, kapasitor \(C\) farads, induktor \(L\) henries, dan sumber tegangan \(E(t)\) memenuhi persamaan
\[
E(t) = LI'(t) + RI(t) + \frac{1}{C} \int I(t) dt
\]
Seperti yang terlihat pada gambar di bawah, arus \(I_1(t)\) dan \(I_2(t)\) di kiri dan kanan loop, berturut-turut, dari rangkaian menunjukan bahwa solusinya adalah
\[\begin{split}
2I_1(t) + 6(I_1(t) - I_2(t)) + 2I_1'(t) = 12, \\
\frac{1}{0.5} \int I_2(t) dt + 4I_2(t) + 6(I_2(t) - I_1(t)) = 0.
\end{split}\]

Jika switch di rangkaian tertutup pada waktu \(t=0\), kita dapatkan kondisi awal \(I_1(0) = 0\) dan \(I_2(0) = 0\). Selesaikan \(I'(t)\) pada persamaan pertama, turunkan persamaan kedua, dan subtitusi \(I_1'(t)\) kita dapatkan
\[\begin{split}
\begin{align}
I_1' &= f_1(t, I_1, I_2) &=& -4I_1 + 3I_2 + 6, I_1(0) = 0, \\
I_2' &= f_2(t, I_1, I_2) &=& 0.6I_1' - 0.2 I_2 = -2.4I_1 + 1.6I_2 + 3.6, I_2(0) = 0.
\end{align}
\end{split}\]
Solusi eksaknya adalah
\[\begin{split}
\begin{align}
I_1(t) &= -3.375 e^{-2t} + 1.875 e^{-0.4t} + 1.5, \\
I_2(t) &= -2.25 e^{-2t} + 2.25 e^{-0.4t}.
\end{align}
\end{split}\]
import numpy as np
import math
import matplotlib.pyplot as plt
%matplotlib inline
T = 20
h = 0.1
N = int(T/h)
t = np.zeros(N+2)
eksak1 = np.zeros(N+1)
eksak2 = np.zeros(N+1)
for i in range(N+1):
eksak1[i] = -3.375*math.exp(-2*t[i]) + 1.875*math.exp(-0.4*t[i]) + 1.5
eksak2[i] = -2.25*math.exp(-2*t[i]) + 2.25*math.exp(-0.4*t[i])
t[i+1] = t[0] + (i+1)*h
def f1(t,I1,I2):
return -4*I1 + 3*I2 + 6
def f2(t,I1,I2):
return -2.4*I1 + 1.6*I2 + 3.6
#RK4
t = np.zeros(N+1)
F = [f1, f2]
K = np.zeros((4, len(F)))
I = np.zeros((N+1,2))
for i in range(N):
for j in range(len(F)):
K[0,j] = h*F[j](t[i], I[i,0], I[i,0])
for j in range(len(F)):
K[1,j] = h*F[j](t[i] + 0.5*h, I[i,0] + 0.5*K[0,0], I[i,1] + 0.5*K[0,1])
for j in range(len(F)):
K[2,j] = h*F[j](t[i] + 0.5*h, I[i,0] + 0.5*K[1,0], I[i,1] + 0.5*K[1,1])
for j in range(len(F)):
K[3,j] = h*F[j](t[i] + h, I[i,0] + K[2,0], I[i,1] + K[2,1])
for j in range(len(F)):
I[i+1,j] = I[i,j] + (1/6)*(K[0,j] + 2*K[1,j] + 2*K[2,j] + K[3,j])
t[i+1] = t[0] + (i+1)*h
#fig, axs = plt.subplots(2, 1)
#axs[0].plot(t, eksak1, label="Solusi Eksak")
#axs[0].plot(t, I[:,0], '-o', label="Solusi RK4")
#axs[0].set_title('$I_1$')
#axs[1].plot(t, eksak2, label="Solusi Eksak")
#axs[1].plot(t,I[:,1], '-o', label="Solusi RK4")
#axs[1].set_title('$I_2$')
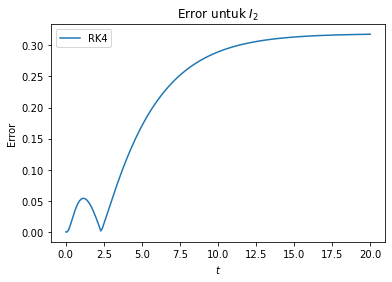
plt.title('Solusi Eksak vs Solusi RK4')
plt.xlabel('$t$')
plt.ylabel('$I_1(t)$')
plt.plot(t, eksak1, label="Solusi Eksak")
plt.plot(t, I[:,0], '-o', label="Solusi RK4")
plt.legend(loc=4)
<matplotlib.legend.Legend at 0x117e05400>
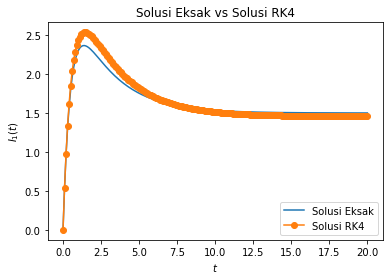
plt.title('Solusi Eksak vs Solusi RK4')
plt.xlabel('$t$')
plt.ylabel('$I_2(t)$')
plt.plot(t, eksak2, label="Solusi Eksak")
plt.plot(t, I[:,1], '-o', label="Solusi RK4")
plt.legend(loc=4)
<matplotlib.legend.Legend at 0x117e34220>
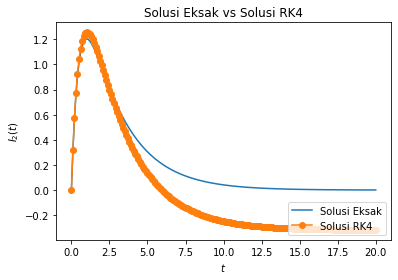
error_rk4 = np.abs(eksak1-I[:,0])
plt.title('Error untuk $I_1$')
plt.xlabel('$t$')
plt.ylabel('Error')
plt.plot(t,error_rk4, label="RK4")
plt.legend()
<matplotlib.legend.Legend at 0x1201f22e0>
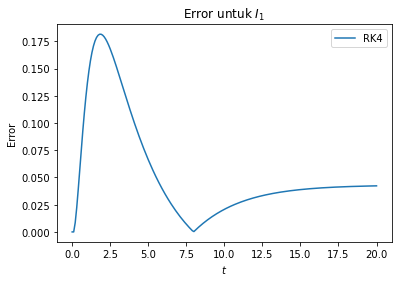
error_rk4 = np.abs(eksak2-I[:,1])
plt.title('Error untuk $I_2$')
plt.xlabel('$t$')
plt.ylabel('Error')
plt.plot(t,error_rk4, label="RK4")
plt.legend()
<matplotlib.legend.Legend at 0x120264610>