Sistem Floating-Point
Contents
Sistem Floating-Point¶
Bilangan di sistem floating-point direpresentasikan sebagai deret dari bit dimana bit-bit tersebut merepresentasikan suatu angka yang berbeda. Secara umum, sistem floating-point ternormalisasi dapat ditulis sebagai
dimana
\(\pm\) adalah bit yang merepresentasikan tanda dari bilangan
\(d_1 . d_2 d_3 d_4 \ldots d_t\) disebut mantissa. The digits \(d_2 d_3 d_4 \ldots d_p\) disebut the fraction/fraksi dengan \(t\) digit presisi. Sistem ternormalisasi secara spesifik \(d_1 \neq 0\) kecuali bilangan tersebut adalah \(0\).
\(\beta\) adalah basis. Untuk binary \(\beta = 2\), untuk desimal \(\beta = 10\), dst.
\(E\) adalah eksponen, suatu bilangan bulat antara \([E_{\min}, E_{\max}]\).
Bagian penting dalam sistem floating-point yaitu
Terdapat himpunan diskrit dan berhingga yang merepresentasikan suatu bilangan
Dapat merepresentasikan bilangan yang tidak terdisrtibusi secara teratur pada garis bilangan (real)
Aritmatika di dalam sistem floating-point menghasilkan hasil yang berbeda dibandingkan dengan aritmatika di dalam sistem bilangan real
Sifat-Sifat dari sistem floating-point
Semua sistem floating-point juga berupa beberapa bilangan yang penting:
Bilangan ternormalisasi terkecil (underflow)
Bilangan ternormalisasi terbesar (overflow)
Nol
Machine \(\epsilon\) atau \(\epsilon_{\text{machine}}\)
infdannan, tak hingga dan Not a Number
Contoh: Misalkan terdapat sistem desimal 2-digit (ternormalisasi)
dengan \(E \in [-2, 0]\).
Bilangan dan distribusi dari bilangan
Berapa banyak bilangan yang dapat direpresentasikan dengan sistem ini?
Bagaimana distribusinya pada garis bilangan “real”?
Apa nilai dari underflow dan overflow?
Berapa banyak bilangan yang dapat direpresentasikan dengan sistem ini?
import matplotlib.pyplot as plt
nilai_d1 = [1, 2, 3, 4, 5, 6, 7, 8, 9]
nilai_d2 = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
nilai_E = [0, -1, -2]
fig = plt.figure(figsize=(10.0, 1.0))
ax = fig.add_subplot(1, 1, 1)
for E in nilai_E:
for d1 in nilai_d1:
for d2 in nilai_d2:
ax.plot( (d1 + d2 * 0.1) * 10**E, 0.0, 'r+', markersize=20)
ax.plot(-(d1 + d2 * 0.1) * 10**E, 0.0, 'r+', markersize=20)
ax.plot(0.0, 0.0, '+', markersize=20)
ax.plot([-10.0, 10.0], [0.0, 0.0], 'k')
ax.set_title("Distribusi Nilai")
ax.set_yticks([])
ax.set_xlabel("x")
ax.set_ylabel("")
ax.set_xlim([-2, 2])
plt.show()

Apa nilai dari underflow dan overflow?
Bilangan terkecil dapat direpresentasikan dengan underflow: \(1.0 \times 10^{-2} = 0.5\)
Bilangan terbesar dapat direpresentasikan dengan overflow: \(1.9 \times 10^0 = 1.9\)
Catatan bahwa semua sistem floating-point IEEE 754 menggunakan bilangan binari.
Cara cepat: $\( 2^3 2^2 2^1 2^0 . 2^{-1} 2^{-2} 2^{-3} \)$ melambangkan 8, 4, 2, 1 . 1/2, 1/4, 1/8, …
Real Systems - IEEE 754 Binary Floating Point Systems¶
Single Precision¶
Total storage yang dialokasi adalah 32 bit
Eksponen is 8 bit \(\Rightarrow E \in [-126, 127]\)
Fraksi 23 bit (\(p = 24\))
s EEEEEEEE FFFFFFFFFFFFFFFFFFFFFFF
0 1 8 9 31
Overflow \(= 2^{127} \approx 3.4 \times 10^{38}\)
Underflow \(= 2^{-126} \approx 1.2 \times 10^{-38}\)
\(\epsilon_{\text{machine}} = 2^{-23} \approx 1.2 \times 10^{-7}\)
Double Precision¶
Total storage yang dialokasi adalah 64 bit
Eksponen is 11 bit \(\Rightarrow E \in [-1022, 1024]\)
Fraksi 52 bit (\(p = 53\))
s EEEEEEEEEE FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FF
0 1 11 12 63
Overflow \(= 2^{1024} \approx 1.8 \times 10^{308}\)
Underflow \(= 2^{-1022} \approx 2.2 \times 10^{-308}\)
\(\epsilon_{\text{machine}} = 2^{-52} \approx 2.2 \times 10^{-16}\)
IEEE Numbers di Python¶
Informasi mengenai parameter-parameter penting terkait dengan sistem floating-point, seperti machine epsilon:
numpy.finfo(float).eps
import numpy
print(numpy.finfo(numpy.float16))
print(numpy.finfo(numpy.float32))
Machine parameters for float16
---------------------------------------------------------------
precision = 3 resolution = 1.00040e-03
machep = -10 eps = 9.76562e-04
negep = -11 epsneg = 4.88281e-04
minexp = -14 tiny = 6.10352e-05
maxexp = 16 max = 6.55040e+04
nexp = 5 min = -max
smallest_normal = 6.10352e-05 smallest_subnormal = 5.96046e-08
---------------------------------------------------------------
Machine parameters for float32
---------------------------------------------------------------
precision = 6 resolution = 1.0000000e-06
machep = -23 eps = 1.1920929e-07
negep = -24 epsneg = 5.9604645e-08
minexp = -126 tiny = 1.1754944e-38
maxexp = 128 max = 3.4028235e+38
nexp = 8 min = -max
smallest_normal = 1.1754944e-38 smallest_subnormal = 1.4012985e-45
---------------------------------------------------------------
print(numpy.finfo(float))
Machine parameters for float64
---------------------------------------------------------------
precision = 15 resolution = 1.0000000000000001e-15
machep = -52 eps = 2.2204460492503131e-16
negep = -53 epsneg = 1.1102230246251565e-16
minexp = -1022 tiny = 2.2250738585072014e-308
maxexp = 1024 max = 1.7976931348623157e+308
nexp = 11 min = -max
smallest_normal = 2.2250738585072014e-308 smallest_subnormal = 4.9406564584124654e-324
---------------------------------------------------------------
Contoh¶
eps = numpy.finfo(float).eps
MAX = numpy.finfo(float).max
print('eps = {}'.format(eps))
print('MAX = {}'.format(MAX))
eps = 2.220446049250313e-16
MAX = 1.7976931348623157e+308
Tunjukan bahwa \((1 + \epsilon_{mach}) > 1\)
print(MAX*1)
print(MAX*(1+eps))
1.7976931348623157e+308
inf
/var/folders/d8/_nrt2sy9567f87n08gxx0xc00000gn/T/ipykernel_2454/1801764505.py:2: RuntimeWarning: overflow encountered in double_scalars
print(MAX*(1+eps))
Kenapa kita perlu mengetahuinya?¶
Aritmatika Floating point tidak komutatif atau asosiatif
Mencampur presisi berbahaya
Contoh 1: Aritmatika Sederhana¶
Aritmatika sederhana \(\delta < \epsilon_{\text{machine}}\)
eps = numpy.finfo(float).eps
delta = 0.5*eps
print('eps = {}, 1 + eps > 1 is {}'.format(eps,((1. + eps) > 1.)))
print('delta = {}, 1 + delta > 1 is {}'.format(delta,((1. + delta) > 1.)))
x = 1+delta -1
y = 1 - 1 + delta
print()
print('1 + delta - 1 = {}'.format(x))
print('1 - 1 + delta = {}'.format(y))
eps = 2.220446049250313e-16, 1 + eps > 1 is True
delta = 1.1102230246251565e-16, 1 + delta > 1 is False
1 + delta - 1 = 0.0
1 - 1 + delta = 1.1102230246251565e-16
import sympy
sympy.init_printing(pretty_print=True)
x = sympy.symbols('x')
f = sympy.exp(x)
f.series(x0=0, n=3)
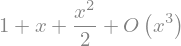
x = 1.
Tn = 1 + x + x**2/2 # solusi aproksimasi dari f(x) = e^x
f = numpy.exp(1.) # nilai eksak
E_t = numpy.abs(f - Tn) # nilai error absolut
epsilon_t = E_t/f # nilai error relatif
print("T_n = {}, E_t = {}, epsilon_t = {}". format(Tn, E_t, epsilon_t))
T_n = 2.5, E_t = 0.2182818284590451, epsilon_t = 0.08030139707139415
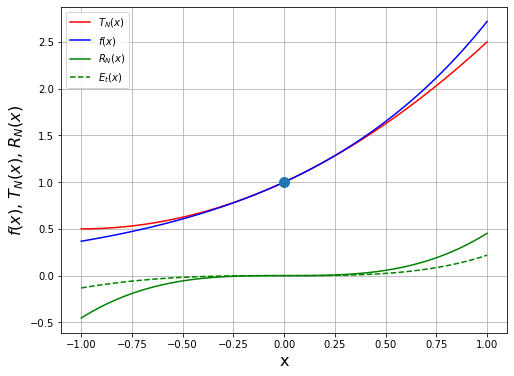
x = numpy.linspace(-1, 1, 100) # membuat sumbu-x
f = numpy.exp(x) # nilai eksak
T_N = 1.0 + x + x**2/2.0
R_N = numpy.exp(1) * x**3/6.0
plt.figure(figsize=(8,6))
plt.plot(x, T_N, 'r', x, f, 'b', x, R_N, 'g')
plt.plot(x, numpy.exp(x) - T_N, 'g--')
plt.plot(0.0, 1.0, 'o', markersize=10)
plt.grid()
plt.xlabel('x', fontsize=16)
plt.ylabel("$f(x)$, $T_N(x)$, $R_N(x)$", fontsize=16)
plt.legend(["$T_N(x)$", "$f(x)$", "$R_N(x)$", "$E_t(x)$"], loc=2)
plt.show();