6. Error di Interpolasi Polynomial#

Kita telah mempelajari interpolasi polynomial, interpolasi Lagrange, dan interpolasi Newton untuk mencari suatu fungsi yang menginterpolasi titik-titik data. Sekarang kita akan membahas tentang error di interpolasi polynomial.

Diberikan suatu fungsi \(f(x)\) dan \(x \in [a, b]\). Suatu himpunan titik \(x_i \in X\), \(i = 0, 1, \cdots, n\) dan \(x_i \in [a, b]\). Misalkan \(P_n(x)\) adalah polynomial berderajat \(n\) yang menginterpolasi \(f(x)\) pada \(x_i\)

\[ P_n(x_i) = f(x_i), \hspace{1em} i = 0, 1, \cdots, n. \]

Definisikan error

\[ e(x) = f(x) - P_n(x) \]

Teorema: Error di Interpolasi Polynomial

Terdapat suatu titik \(\xi \in [a,b]\) sedemikian sehingga

\[ \label{3} e(x) = \frac{1}{(n+1)!} f^{(n+1)} (\xi) \prod_{i=0}^{n} (x-x_i), \hspace{1em} \forall x \in [a,b].\]

Bukti

Jika \(f \in \mathcal{P}_n\) maka \(f(x) = P_n(x)\), trivial. Sekarang asumsikan \(f \notin \mathcal{P}_n\). Untuk \(x = x_i\), kita punya \(e(x_i) = f(x_i) - P_n(x_i) = 0\), OK. Sekarang kita asumsikan terdapat \(a\) sedemikian sehingga \(a \neq x_i\). Kita definisikan

\[ \label{4} W(x) = \prod_{i=0}^{n} (x - x_i) \in \mathcal{P}_{n+1}\]

dan konstanta

\[ c = \frac{f(a) - P_n(a)}{W(a)},\]

dan fungsi lain

\[ \varphi(x) = f(x) - P_n(x) - cW(x).\]

Kita ingin mencari semua bernilai nol untuk fungsi \(\varphi\):

\[ \varphi(x_i) = f(x_i) - P_n(x_i) - cW(x_i) = 0, \hspace{1em} i = 0, 1, \cdots, n \]

dan

\[ \varphi(a) = f(a) - P_n(a) - cW(a) = 0.\]

Jadi, \(\varphi\) memiliki paling sedikit \((n+2)\) bernilai nol. Berdasarkan bahwa terdapat suatu bilangan \(\xi \in (a,b)\) sehingga kita dapatkan

\[ \varphi^{(n+1)}(\xi) = f^{(n+1)}(\xi) - 0 - cW^{(n+1)}(\xi) = 0.\]

Dari kita tahu bahwa

\[ W^{(n+1)} = (n + 1)!.\]

Sehingga kita dapatkan

\[f^{(n+1)}(\xi) = cW^{(n+1)}(\xi) = \frac{f(a) - P_n(a)}{W(a)}(n+1)!.\]

Kita ubah \(a\) menjadi \(x\), maka didapatkan

\[ e(x) = f(x) - P_n(x) = \frac{1}{(n+1)!} f^{(n+1)} (\xi) W(x) = \frac{1}{(n+1)!} f^{(n+1)} (\xi) \prod_{i=0}^{n} (x-x_i).\]

6.1. Contoh 1#

\[f(x) = \cos(x)\]

dengan \(x_0 = 0, x_1 = 0.6, x_2 = 0.9.\)

Cari turunan

\[\begin{split} \begin{align*} f'(x) &= -\sin(x) \\ f''(x) &= -\cos(x) \\ f'''(x) &= \sin(x) \end{align*} \end{split}\]

Polynomial Lagrange orde 2:

\[ \frac{f'''(\xi)}{3!}(x-x_0)(x-x_1)(x-x_2) = \frac{\sin(\xi)}{6}(x-0)(x-0.6)(x-0.9), \hspace{1em} \xi \in (0, 0.9). \]

Nilai maksimum dari \(\sin(\xi)\) pada selang tersebut adalah \(\sin(0.9)=0.7833\). Nilai maksimum dari \(g(x) = (x-0)(x-0.6)(x-0.9) = (x^3 - 1.5x^2 + 0.54x)\) dapat dicari dengan mencari turunan pertama

\[ g'(x) = 2x^2 - 3x + 0.54 = 0. \]

Sehingga didapat titik kritisnya yaitu: \(g'(0.2092)=2(0.2092)^2 - 3(0.2092) + 0.54 = -0.0438\) dan \(g'(1.291)=2(1.291)^2 - 3(1.291) + 0.54 = -1.6663.\)

Jadi, error maksimumnya adalah:

\[\left| \frac{\sin(\xi)}{6}(x-0)(x-0.6)(x-0.9)\right| \leq \left| \frac{0.7833}{6} -0.0438 \right| = 0.0057.\]

Polynomial Lagrange orde 1:

\[ \frac{f''(\xi)}{2!}(x-x_0)(x-x_1) = \frac{\sin(\xi)}{6}(x-0)(x-0.6), \hspace{1em} \xi \in (0, 0.6). \]

6.2. Contoh 2#

Diberikan \(x_0 = a, x_1 = b, b > a\) dan \(n = 1\). Kita punya batas atas errornya berdasarkan untuk \(x \in [a,b]\) yaitu

\[ \label{contoh_1} |e(x)| = \left| \frac{f''(\xi)}{2!} (x-a) (x-b) \right| \leq \frac{\lVert f'' \rVert_{\infty}}{2!} \frac{(b-a)^2}{4} = \frac{1}{8} \lVert f'' \rVert_{\infty} (b-a)^2. \]

Catatan: \(\lVert f(\xi) \rVert_{\infty} = \max_{\xi \in (a,b)} (f(\xi))\) biasanya ini dipakai untuk menyatakan norm pada suatu vektor, tapi disini kita pakai untuk mencari nilai maksimum dari suatu fungsi pada suatu interval.

Note

Berdasarkan kita dapat fakta bahwa distribusi titik \(x_i\) yang berbeda akan menghasilkan error yang berbeda juga. Dengan kata lain, error yang dihasilkan pada suatu interpolan dipengaruhi oleh distribusi titik.

6.3. Titik yang seragam#

Misalkan teradapat suatu selang \([a,b]\) dan kita ingin menyebar \((n+1)\) titik secara seragamd dengan

\[x_i = a + ih, \hspace{1em} i = 0, 1, \cdots, n\]

dimana \(h = \frac{b-a}{n}\). Kita dapat mengukur error interpolasi di setiap titiknya jika diberikan \(n\) dan berdasarkan

\[ \prod_{i=0}^{n} |x - x_i| \leq \frac{1}{4} h^{n+1} n!.\]

Maka errornya dapat diestimasi dengan

\[|e(x)| \leq \frac{1}{4(n+1)} |f^{(n+1)}(x)| h^{n+1} \leq \frac{M_{n+1}}{4(n+1)} h^{n+1} \]

dimana

\[ M_{n+1} = \max_{x\in [a,b]} |f^{(n+1)}(x)|.\]

6.4. Contoh 3#

Misalkan kita ingin menginterpolasi \(f(x) = \sin(\pi x)\) dengan suatu polynomial pada interval \([-1,1]\) dengan titik yang seragam. Tentukan batas atas dari error yang dihasilkan polynomial tersebut.

Ingin: mencari batas atas dari \(|e(x)|\)

\[|f^{(n+1)(x)}| \leq \pi^{n+1} \]

batas atas errornya

\[|e(x)| = |f(x) - P_n(x)| \leq \frac{\pi^{n+1}}{4(n+1)} \left( \frac{2}{n} \right)^{n+1}\]

6.5. Kasus 1: Equally spaced#

using Plots
using Polynomials

N = 20
x = range(0, 5, length=N)
y = sin.(π*x);

scatter(x, y, label="titik data",
    xlabel="x",
    ylabel="y"
)

6.5.1. Interpolasi Polynomial#

V = [x[i]^j for i=1:length(x), j=0:length(x)-1]
a = V \ y
p = Polynomial(a)
3.143585817762968∙x - 0.026733845340492383∙x2 - 5.0114309035624265∙x3 - 0.5368070278937∙x4 + 3.7763574671015396∙x5 - 1.9921042714233053∙x6 + 1.7986044647582435∙x7 - 2.194540117942741∙x8 + 1.6338185344371865∙x9 - 0.8547102637598286∙x10 + 0.3599381786536144∙x11 - 0.12241046899364212∙x12 + 0.03160439500175783∙x13 - 0.005858509473200379∙x14 + 0.0007447727658999214∙x15 - 6.104763914190642e-5∙x16 + 2.8414109131835047e-6∙x17 - 4.979474072491975e-8∙x18 - 5.501913770861472e-10∙x19
xx = range(0, 5, length=100)
yy = p.(xx)
scatter(x, y, label="titik data",
    xlabel="x",
    ylabel="y"
)
plot!(xx, yy, label="interpolasi polynomial", linewidth=2)

6.5.2. Interpolasi Lagrange#

function Lagrange_basis(x_data)
    n = length(x_data)
    L = zeros(n, n)
    for i in 1:n
        for j in 1:n
            if i == j
                L[i, j] = 1.0
            else 
                L[i, j] = 0.0
            end
        end
    end
    return L
end

Lagrange_basis (generic function with 1 method)

function poly_Lagrange(x, x_data, koef)
    n = length(x_data)
    hasil = 0.0
    for i in 1:n
        term = koef[i]
        for j in 1:n
            if i != j
                term *= (x - x_data[j]) / (x_data[i] - x_data[j])
            end
        end
        hasil += term
    end
    return hasil
end

poly_Lagrange (generic function with 1 method)

V = Lagrange_basis(x)
a = V \ y
p = poly_Lagrange

poly_Lagrange (generic function with 1 method)

xx = range(0, 5, length=100)
yy = [poly_Lagrange(xx[i], x, a) for i in 1:length(xx)]
scatter(x, y, label="titik data",
    xlabel="x",
    ylabel="y"
)
plot!(xx, yy, label="Interpolasi Lagrange", linewidth=2)

6.6. Contoh: Fungsi Runge#

\[f(x) = \frac{1}{1+25x^2}\]
N = 20
x = [2*i/N - 1 for i=1:N]
y = 1 ./(1 .+ 25 .* x .^ 2);

scatter(x, y, label="titik data",
    xlabel="x",
    ylabel="y"
)

6.6.1. Interpolasi polynomial#

V = [x[i]^j for i=1:length(x), j=0:length(x)-1]
a = V \ y
p = Polynomial(a)
1.000000000093595 - 0.03426081442993426∙x - 24.10921882279521∙x2 + 5.275369726729508∙x3 + 465.570857502395∙x4 - 220.8020592783676∙x5 - 5898.417898899041∙x6 + 3925.7161819686817∙x7 + 45391.826819194735∙x8 - 35581.85546794112∙x9 - 209667.42896345054∙x10 + 179375.945289634∙x11 + 577911.1492082796∙x12 - 520193.35076941084∙x13 - 922751.6161750988∙x14 + 857184.5198762539∙x15 + 781992.8951396744∙x16 - 741509.1002540372∙x17 - 270585.7768843355∙x18 + 260178.63167139245∙x19
xx = range(-1, 1, length=1000)
yy = p.(xx)

scatter(x, y, label="titik data",
    xlabel="x",
    ylabel="y"
)
plot!(xx, yy, label="interpolasi polynomial", linewidth=2, ylimits=(-0.2,1.5))

6.6.2. Interpolasi Lagrange#

V = Lagrange_basis(x)
a = V \ y
p = poly_Lagrange

poly_Lagrange (generic function with 1 method)

xx = range(-1, 1, length=1000)
yy = [poly_Lagrange(xx[i], x, a) for i in 1:length(xx)]
scatter(x, y, label="titik data",
    xlabel="x",
    ylabel="y"
)
plot!(xx, yy, label="Interpolasi Lagrange", linewidth=2, ylimits=(-0.2,1.5))

Gejala ini disebut juga dengan Runge phenomenon.

6.7. Kasus 2: Non equally spaced#

x = [0.9, 1.3, 1.9, 2.1, 2.6, 3.0, 3.9, 4.4, 4.7, 5.0, 6.0, 7.0, 8.0, 9.2, 10.5, 11.3, 11.6, 12.0, 12.6, 13.0, 13.3]
y = [1.3, 1.5, 1.85, 2.12, 2.6, 2.7, 2.4, 2.15, 2.05, 2.11, 2.25, 2.3, 2.26, 1.95, 1.4, 0.9, 0.7, 0.6, 0.5, 0.4, 0.25];

scatter(x, y, label="titik data",
    xlabel="x",
    ylabel="y"
)

6.7.1. Interpolasi polynomial#

V = [x[i]^j for i=1:length(x), j=0:length(x)-1]
a = V \ y
p = Polynomial(a)
-48469.30620187156 + 262495.9459529397∙x - 641099.9457621493∙x2 + 941720.2865776637∙x3 - 935549.466270742∙x4 + 669744.9578982332∙x5 - 359268.58243188105∙x6 + 148175.5131876489∙x7 - 47813.54389018773∙x8 + 12212.549236961178∙x9 - 2487.038321534474∙x10 + 405.21266758365573∙x11 - 52.81562347623002∙x12 + 5.4857905723684945∙x13 - 0.4503083566739462∙x14 + 0.028805190937218485∙x15 - 0.0014041750866934262∙x16 + 5.033874723178627e-5∙x17 - 1.2500599313623058e-6∙x18 + 1.9195836092609337e-8∙x19 - 1.3723931394986858e-10∙x20
xx = range(0, 14, length=1000)
yy = p.(xx)
scatter(x, y, label="titik data",
    xlabel="x",
    ylabel="y"
)
plot!(xx, yy, label="interpolasi polynomial", linewidth=2, ylimits=(-2,4))

6.7.2. Interpolasi Lagrange#

V = Lagrange_basis(x)
a = V \ y
p = poly_Lagrange

poly_Lagrange (generic function with 1 method)

xx = range(0, 14, length=1000)
yy = [poly_Lagrange(xx[i], x, a) for i in 1:length(xx)]
scatter(x, y, label="titik data",
    xlabel="x",
    ylabel="y"
)
plot!(xx, yy, label="Interpolasi Lagrange", linewidth=2, ylimits=(-2,4))

6.8. Lampiran#

6.8.1. Teorema nilai rataan#

Teorema Nilai Rataan

Jika \(f\) adalah fungsi yang kontinu di selang \([a,b]\) dan f terdiferensialkan pada \((a,b)\), maka terdapat bilangan \(c\) di selang \((a, b)\) (lihat ) dengan

\[ f'(c) = \frac{f(b) - f(a)}{b - a}.\]
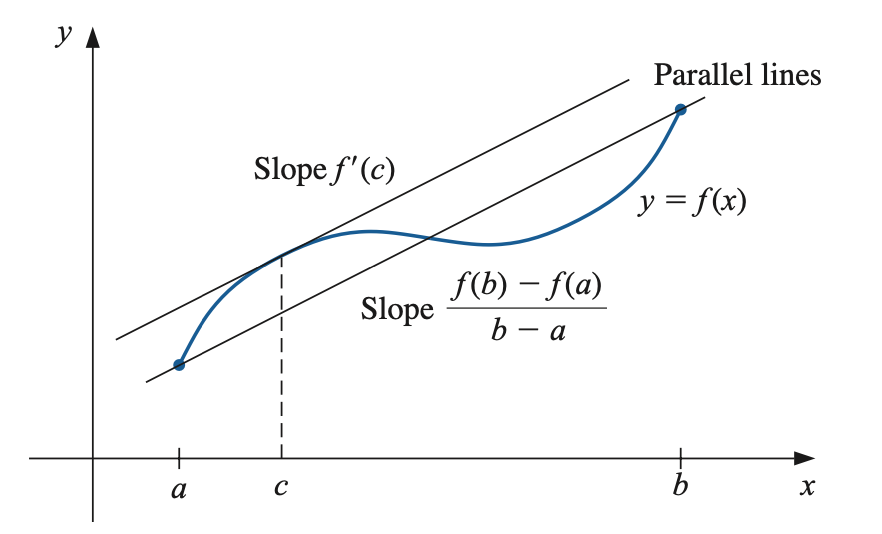
../../_images/mvt.png

Fig. 6.1 Ilustrasi teorema nilai rataan.#

6.8.2. Teorema Rolle#

Teorema Rolle

Misalkan \(f\) kontinu di selang \([a,b]\) dan \(f\) terdiferensialkan pada \((a,b)\). Jika \(f(a) = f(b)\) maka terdapat bilangan \(c\) di selang \((a,b)\) dengan \(f'(c) = 0\). (lihat )

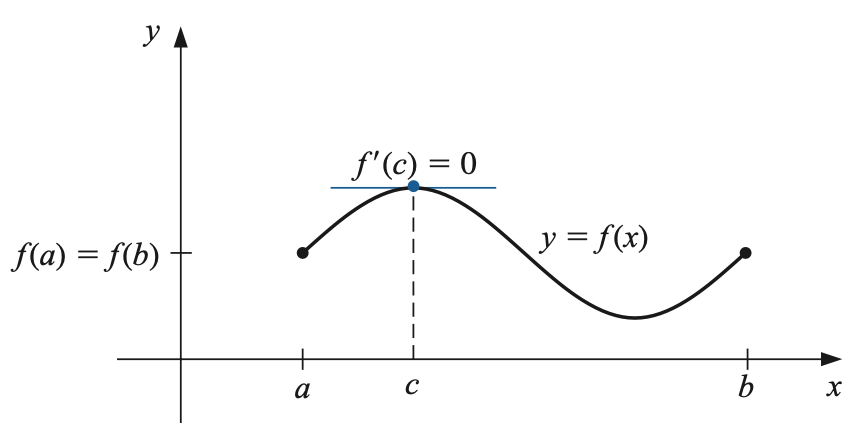
../../_images/rolle.png

Fig. 6.2 Ilustrasi teorema Rolle.#

6.8.3. Teorema Rolle diperumum#

Teorema Rolle Diperumum

Misalkan \(f\) kontinu di selang \([a,b]\) dan \(f\) terdiferensialkan \(n\) kali pada \((a,b)\). Jika \(f(x) = 0\) pada \((n+1)\) nilai berbeda \(a \leq x_0 < x_1 < \cdots < x_n \leq b\) maka terdapat bilangan \(c\) di selang \((x_0,x_n)\) dan juga di \((a,b)\) dengan \(f^{(n)}(c) = 0\).