3. Interpolasi#

Indonesia menyelenggarakan sensus penduduk setiap 10 tahun sekali. Misalkan kita ingin mengetahui jumlah penduduk di antara rentang tersebut. Salah satu caranya adalah mencari suatu polynomial yang melewati titik-titik data tersebut.

3.1. Contoh sederhana#

Diberikan suatu titik (2,5) dan (3,8). Tentukan persamaan garis yang melalui kedua titik tersebut.

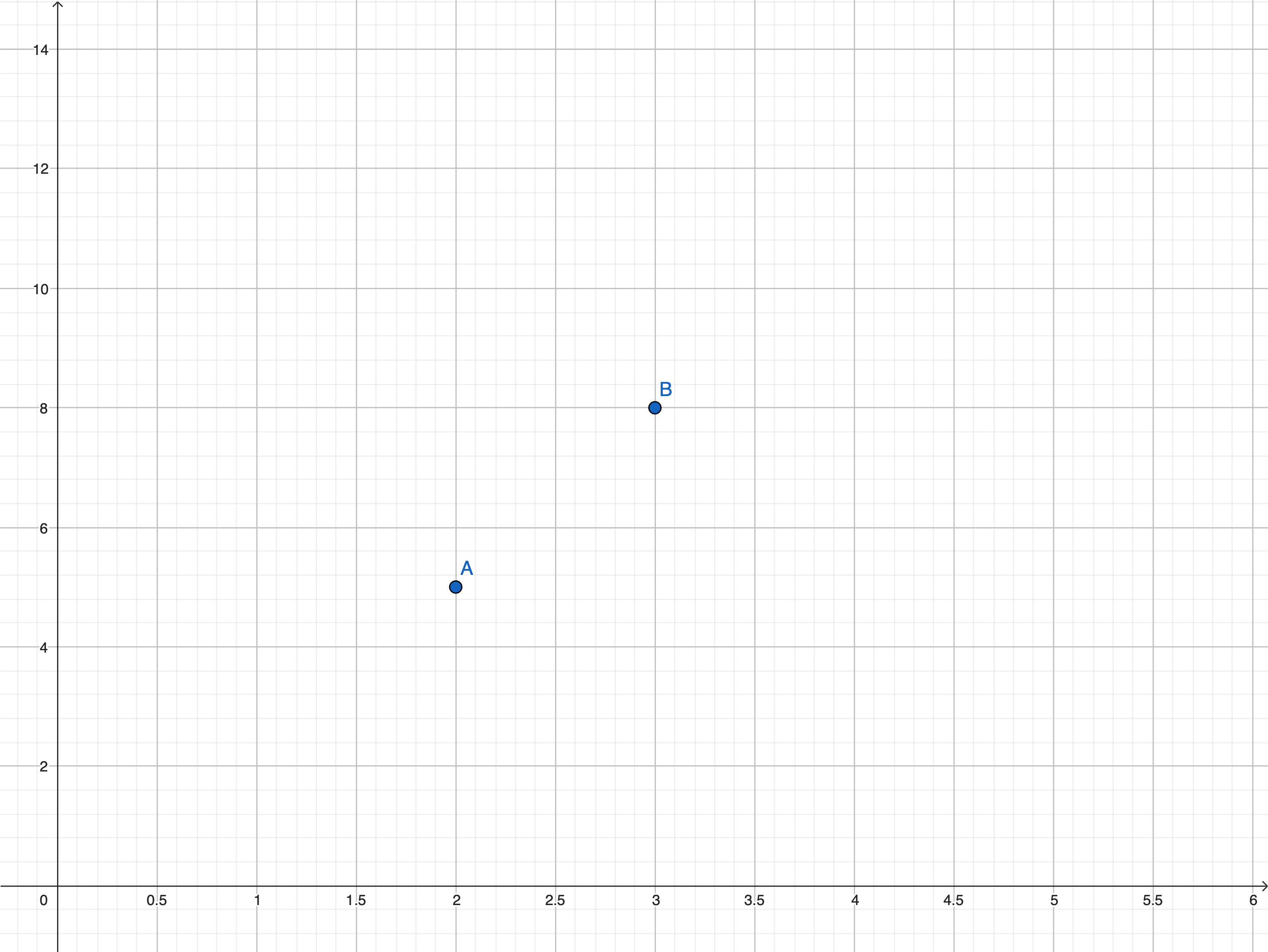
persamaan garis

Jawaban

\[ \label{pers_1} y - y_1 = \frac{y_2 - y_1}{t_2 - t_1} (t - t_1) \]

dan kita punya \(t_1 = 2\), \(t_2 = 3\), \(y_1 = 5\), dan \(y_2 = 8\). Kemudian terapkan ke dalam maka persamaan garisnya adalah

\[\begin{split} \begin{align*} y - 5 &= \frac{8 - 5}{3 - 2} (t - 2)\\ y & = 3t - 1. \end{align*} \end{split}\]

Cara di atas memanfaatkan gradien sebagai acuan kemiringan garis yang melalui dua titik. Lalu bagaimana jika kita ingin mengetahui fungsi apa yang dapat melalui lebih dari dua titik.

Definisi: Interpolasi Polynomial

Diberikan \((n+1)\) titik \((x_0, y_0), (x_1, y_1), \cdots, (x_n, y_n)\), dimana \(x_i\) seluruhnya berbeda, masalah interpolasi polynomial adalah mencari suatu polynomial derajat \(n\), \(P_n(x) = a_0 + a_1 x + \cdots + a_n x^n\), sedemikian sehingga polynomial ini akan menginterpolasi titik data \(\lbrace (x_i, y_i) \rbrace_{i=0}^{n}\) atau dapat ditulis

\[ P_n(x_i) = y_i, \hspace{1em} i = 0, 1, 2, \cdots, n \]

3.2. Interpolasi sebagai sistem linear#

Diberikan data \((x_i, y_i)\) untuk \(i = 0, 1, 2, \cdots, n\). Kita panggil suatu polynomial

\[ \label{polynomial} P_n(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^{n} \]

sedemikian sehingga

\[ \label{poly_y} y_i = P_n(x_i), \hspace{1em} \forall i \]

Dengan kata lain, setiap \(y_i\) diwakili oleh suatu fungsi \(P(x_i)\). Jadi, dengan mensubtitusi ke dalam maka akan membentuk suatu sistem persamaan linear dengan koefisien \(a_0, \cdots, a_n\):

\[\begin{split} \begin{align*} a_0 + a_1 x_0 + \cdots + a_{n}x_0^{n} &= y_0, \\ a_0 + a_1 x_1 + \cdots + a_{n}x_1^{n} &= y_1, \\ & \vdots \\ a_0 + a_1 x_n + \cdots + a_{n}x_n^{n} &= y_n, \\ \end{align*} \end{split}\]

atau dapat ditulis ke dalam persamaan matriks-vektor

\[\begin{split} \begin{bmatrix} 1 & x_0 & \cdots & x_0^{n} \\ 1 & x_1 & \cdots & x_1^{n} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & \cdots & x_n^{n} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_n \end{bmatrix} = \begin{bmatrix} y_0 \\ y_1 \\ \vdots \\ y_n \end{bmatrix} \end{split}\]

atau \(V\textbf{a} = \textbf{y}\), dimana \(V\) disebut juga dengan matriks Vandermonde.

3.3. Contoh 1#

Table 3.1 Titik data#

\(x_i\)

\(y_i\)

0

1

1

0

2/3

0.5
\[\begin{split} \begin{align*} x = 0, y = 1 &: P_2(0) = a_0 = 1 \\ x = 1, y = 0 &: P_2(1) = a_0 + a_1 + a_2 = 0 \\ x = 2/3, y = 0.5 &: P_2(2/3) = a_0 + (2/3)a_1 + (4/9)a_2 = 0.5 \\ \end{align*} \end{split}\]

Sistem persamaan di atas dapat dibentuk ke dalam bentuk persamaan matriks

\[\begin{split} \begin{bmatrix} 1 & 0 & 0 \\ 1 & 1 & 1 \\ 1 & \frac{2}{3} & \frac{4}{9} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0.5 \end{bmatrix} \end{split}\]
using Plots
using Polynomials

x = [0, 1, 2/3]
y = [1, 0, 0.5]

scatter(x, y, label="titik data",
    xlabel="x",
    ylabel="y"
)

V = [x[i]^j for i=1:length(x), j=0:length(x)-1]
V

3×3 Matrix{Float64}:
 1.0  0.0       0.0
 1.0  1.0       1.0
 1.0  0.666667  0.444444

a = V \ y
a

3-element Vector{Float64}:
  1.0
 -0.2500000000000001
 -0.7499999999999999

p = Polynomial(a)
1.0 - 0.2500000000000001∙x - 0.7499999999999999∙x2
xx = range(0, 1, length=100)
yy = p.(xx)
foreach(println, yy[1:length(y)])

1.0
0.997398224670952
0.9946434037343128

plot!(xx, yy, label="interpolant")

3.4. Contoh 2#

Table 3.2 Populasi penduduk di Indonesia#

Tahun

Jumlah

1980

79.2

2000

223.6

2010

260.2

2015

278.2

3.4.1. Plot data#

tahun = [1980, 2000, 2010, 2015]
populasi = [79.2, 223.6, 260.2, 278.2]

t = tahun .- 1980
y = populasi;

scatter(t, y, label="aktual",
    xlabel="sejak tahun 1980",
    ylabel="jumlah penduduk (juta)",
    title="Populasi penduduk di Indonesia"
)

V = [t[i]^j for i=1:4, j=0:3]

4×4 Matrix{Int64}:
 1   0     0      0
 1  20   400   8000
 1  30   900  27000
 1  35  1225  42875

c = V \ y

4-element Vector{Float64}:
 79.2
 11.55904761904761
 -0.2824761904761897
  0.003276190476190462

y - V*c

4-element Vector{Float64}:
 0.0
 0.0
 0.0
 0.0

p = Polynomial(c)
p(2000-1980)

223.6

tt = range(0, 35, length=100)
yy = p.(tt)
foreach(println, yy[1:4])

79.2
83.25137083174018
87.23299841938756
91.14575136117836

plot!(tt, yy, label="interpolant")